Les mensonges de la presse
Re: Les mensonges de la presse
...Mais te prends pas la tête sur ce sujet si tu n'en as pas envie, tkt, pas de souci. Je peux survivre de te voir faire la promo de RMXP. ^^ (que globalement j'aime bien, d'ailleurs) Désolé de t'embêter avec ça.
Re: Les mensonges de la presse
J'ai une collègue dans la grosse boite où je suis prestataire (>10.000 personnes) qui est devenu développeuse Java passée 55 ans. Ca fait 2 ans qu'elle a fait sa reconversion, elle dit tout le temps qu'elle est nulle mais elle maitrise bien. Elle a fait plein de reconversions comme ça dans sa vie, c'est cool.Roi of the Suisse a écrit : ↑28 févr. 2024, 23:51Tu essaies de me faire rentrer dans un débat que je ne comprends même pas, donc je ne peux pas trop t’aider désolé
Mais si tu veux on peut débattre du port du voile en discothèque.
J'ai l'impression que tu vois la programmation comme un mur sacré infranchissable, mais c'est comme : connaître plein de jeux rétros auxquels piquer des sprites, savoir faire une recherche google en anglais, savoir composer de la musique, savoir gribouiller des décors custom, savoir bien programmer en event des choses compliquées, savoir rédiger les dialogues de son jeu en anglais... On pratique un peu et pouf on sait le faire voilà tout. C'est comme toutes les compétences du monde. Ça n'est pas une discipline plus magique que toutes les autres. La programmation te semblait une discipline à part quand tu étais bébé, mais maintenant que tu es grand, tu peux reconsidérer la question, non ?
Quand on n'a pas touché à un domaine, ça nous semble être une montagne, par exemple : la cuisine, le bricolage, mais on suit deux-trois tutoriels sur youtube, on demande conseil au vendeur LeroyMerlin et hop on est le roi du bricolage/cuisine, on sait fixer une étagère ou cuisiner un gratin de chou-fleur. Mais pour des gens qui n'ont aucune notion, c'est complètement mystique, ils ont un blocage, ils ne savent pas par où commencer. Alors qu'en vrai y a rien de sorcier. J'ai eu ma révélation du bricolage il n'y a pas longtemps.
Re: Les mensonges de la presse
Sinon j'ai ENFIN trouvé un article qui explique la back propagation simplement halleluia.
Donc on a le taux d'erreur entre notre résultat voulu et le résultat obtenu, genre 0.2546475.
Avec ce taux, on parcourt chaque neurone, et chacun de ses poids, pour l'informer du taux d'erreur et lui demander de s'ajuster selon une formule.
La formule est bizarre :
laValeurQuOnVaAdditionnerAuPoids = poids * (-tauxDErreurDerniereEpoque) * derniereSortieNeurone * tauxDErreurDerniereEpoque * (1-tauxDErreurDerniereEpoque);
poids = poids + laValeurQuOnVaAdditionnerAuPoids;
Trouvée ici : https://www.nnwj.de/backpropagation.html
Merci merci merci des maths simples !!!!
Néanmoins je comprends pas la formule mais oh bon tant pis
Je crois que c'est équivalent à cet article https://neptune.ai/blog/backpropagation ... orks-guide :
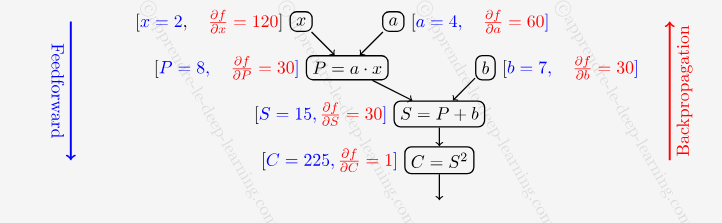
https://apprendre-le-deep-learning.com/ ... opagation/
Mais sérieux ?!!! C'est pas plus simple comme je l'ai écrit ?!!! Comment vous voulez qu'on comprenne ça aaaaaaaaaaaaaaahhhhhhhhh
En tout cas effectivement j'ai l'impression que le réseau apprend beaucoup plus vite quand on lui applique cette formule magique.
Donc on a le taux d'erreur entre notre résultat voulu et le résultat obtenu, genre 0.2546475.
Avec ce taux, on parcourt chaque neurone, et chacun de ses poids, pour l'informer du taux d'erreur et lui demander de s'ajuster selon une formule.
La formule est bizarre :
laValeurQuOnVaAdditionnerAuPoids = poids * (-tauxDErreurDerniereEpoque) * derniereSortieNeurone * tauxDErreurDerniereEpoque * (1-tauxDErreurDerniereEpoque);
poids = poids + laValeurQuOnVaAdditionnerAuPoids;
Trouvée ici : https://www.nnwj.de/backpropagation.html
Merci merci merci des maths simples !!!!
Néanmoins je comprends pas la formule mais oh bon tant pis
Je crois que c'est équivalent à cet article https://neptune.ai/blog/backpropagation ... orks-guide :
Et équivalent à ça ???W(n+1)=W(n)+η[d(n)-Y(n)]X(n)
Where:
n: Training step (0, 1, 2, …).
W(n): Parameters in current training step. Wn=[bn,W1(n),W2(n),W3(n),…, Wm(n)]
η: Learning rate with a value between 0.0 and 1.0.
d(n): Desired output.
Y(n): Predicted output.
X(n): Current input at which the network made false prediction.

https://apprendre-le-deep-learning.com/ ... opagation/
Mais sérieux ?!!! C'est pas plus simple comme je l'ai écrit ?!!! Comment vous voulez qu'on comprenne ça aaaaaaaaaaaaaaahhhhhhhhh
En tout cas effectivement j'ai l'impression que le réseau apprend beaucoup plus vite quand on lui applique cette formule magique.
Modifié en dernier par trotter le 05 mars 2024, 19:28, modifié 1 fois.
- Roi of the Suisse
- Messages : 2105
- Enregistré le : 28 avr. 2019, 23:38
- Contact :
Re: Les mensonges de la presse
Beh la formule parle de la sortie (résultat) des neurones i et i+1, et toi dans ton message tu parles de l'erreur :trotter a écrit : ↑02 mars 2024, 19:40La formule est bizarre :
laValeurQuOnVaAdditionnerAuPoids = poids * (-tauxDErreurDerniereEpoque) * poids * tauxDErreurDerniereEpoque * (1-tauxDErreurDerniereEpoque);
poids = poids + laValeurQuOnVaAdditionnerAuPoids;
Trouvée ici : https://www.nnwj.de/backpropagation.html
nouveau poids = ancien poids + taux d'apprentissage * erreur de la sortie * sortie du neurone i * sortie du neurone i+1 * (1 - sortie du neurone i+1)Change all weight values of each weight matrix using the formula
weight(old) + learning rate * output error * output(neurons i) * output(neurons i+1) * ( 1 - output(neurons i+1) )
La sortie (output) c'est le résultat du calcul effectué par le neurone. L'erreur, c'est une note qui mesure l'écart entre le résultat et la vraie bonne réponse.
Tu es sûr de ton coup ?
Re: Les mensonges de la presse
Fuck non, déjà j'avais codé :
laValeurQuOnVaAdditionnerAuPoids = poids * (-tauxDErreurDerniereEpoque) * derniereSortieNeurone * tauxDErreurDerniereEpoque * (1-tauxDErreurDerniereEpoque);
...contrairement à ce que j'ai écrit ici (j'ai édité).
.....mais en plus il me manque cette notion de neurone i+1
Bon c'est reparti sur le drawing board.
Merci !!!!!!!
laValeurQuOnVaAdditionnerAuPoids = poids * (-tauxDErreurDerniereEpoque) * derniereSortieNeurone * tauxDErreurDerniereEpoque * (1-tauxDErreurDerniereEpoque);
...contrairement à ce que j'ai écrit ici (j'ai édité).
.....mais en plus il me manque cette notion de neurone i+1
Bon c'est reparti sur le drawing board.
Merci !!!!!!!
Re: Les mensonges de la presse
J'abuse un peu gentil ROTS mais si c'est pas trop galère pour toi* tu pourrais m'expliquer comme si j'avais 12 ans comment cette formule magique "corrige" les poids des neurones ? Et est-ce qu'il faut l'appliquer aux biais aussi ?
*Je sais pas si pour toi qui fait des maths ça apparait totalement évident comment ça marche ou bien s'il te faut quand même un effort, te plonger dans le truc etc dans ce cas t'embête pas je veux pas abuser.
*Je sais pas si pour toi qui fait des maths ça apparait totalement évident comment ça marche ou bien s'il te faut quand même un effort, te plonger dans le truc etc dans ce cas t'embête pas je veux pas abuser.
- Roi of the Suisse
- Messages : 2105
- Enregistré le : 28 avr. 2019, 23:38
- Contact :
Re: Les mensonges de la presse
Je peux essayer d'interpréter la formule et de raconter ce qu'elle fait, mais comme je ne suis pas spécialiste des réseaux de neurones, je ne garantis pas à 100% que ça soit l'explication officielle :
weight(old) + learning rate * output error * output(neurons i) * output(neurons i+1) * ( 1 - output(neurons i+1) )
weight(old) + on veut modifier le poids actuel, pas le remplacer complètement, donc on part de l'ancien poids, et on l'augmente un peu ou bien on le réduit un peu. On veut converger progressivement vers le réseau optimal. Si on remplace absolument tout à chaque étape, on ne saura pas dire si on va dans la bonne direction / si on s'améliore, parce que le réseau perdrait la "mémoire" de ses précédentes tentatives avec lesquelles comparer la tentative actuelle.
learning rate * c'est un paramètre arbitraire qui dit à quelle vitesse le réseau va prendre en compte ses erreurs, ici le mec a mis 0,25. Si tu mets plus, le réseau va beaucoup prendre en compte ses erreurs pour se corriger ; si tu mets moins le réseau va attendre de commettre beaucoup d'erreurs avant de se dire qu'il faut changer quelque chose. On voit bien dans la formule que plus le learning rate est grand, plus le poids va être modifié.
Il me semble que si le learning rate est grand, le réseau va converger vite, mais pas forcément vers LE réseau optimal. Alors que si le learning rate est faible, le réseau va converger lentement, mais potentiellement il sera à la fin beaucoup plus proche DU réseau optimal.
C'est un juste milieu, il faut expérimenter avec différents learning rates et trouver celui qui a l'air de fournir des résultats acceptables sans avoir à attendre 10 000 ans.
output error * c'est normal qu'il faille modifier le poids d'autant plus que l'erreur est grande. Si le poids est pas bon du tout, il faut le changer beaucoup ; si le poids est juste un petit peu faux, il faut l'ajuster légèrement. C'est le morceau le plus évident de la formule.
output(neurons i) * c'est le résultat de la couche précédente, que le neurone courant multiplie par son poids, le poids qu'on est justement en train d'essayer d'ajuster. Donc si ce résultat (venant de l'amont) était grand, il a une grande incidence sur le résultat de notre neurone courant. Ici il faut bien imaginer que notre neurone courant reçoit plusieurs résultats de la couche en amont : des petits résultats 0.0123 et des grands résultats 0.9987, et que pour chacun de ces résultats qu'on lui fournit, notre neurone courant a un poids. Les résultats de la couche amont (qui sont les entrées de notre neurone courant) n'ont pas tous le même impact sur le résultat produit : les grands résultats auront plus d'impact. Notre neurone courant reçoit 0,00012 0,0001 0,895 0,784, il va multiplier tout ça par des poids et les additionner, eh bien les deux derniers auront beaucoup d'importance dans son calcul, on peut carrément négliger les deux premiers tellement ils sont ridicules. Donc si notre neurone s'est trompé, c'est surtout à cause des branches qui ont fourni les grands résultats, et des poids de ces branches. Les branches qui ont passé les grands résultats sont plus "coupables" de l'erreur que les branches qui ont passé de petits résultats. C'est pourquoi la formule change davantage le poids d'une branche qui a fourni une grande valeur.
output(neurons i+1) * ( 1 - output(neurons i+1) ) cette dernière partie, je la traiterais un en seul bloc. En gros c'est la fonction x*(1-x) appliquée au résultat produit par notre neurone courant. Que fait cette fonction x*(1-x) ? Si on met une valeur extrême dedans, elle sort un petit nombre : 0,01 * 0,99 = 0,0099 ; et si on lui donne une valeur moyenne, elle sort un grand nombre : 0,5 * 0,5 = 0,25. Il faut bien voir que 0,25 est beaucoup plus grand que 0,0099. Donc en gros, le poids sera d'autant plus modifié que notre neurone courant a produit un résultat moyen. Ici, mon interprétation est qu'on veut que notre neurone produise des résultats bien tranchés (0,001 ou 0,999) et pas des 0,5 tout mous. Comme s'il y avait un postulat qu'un neurone était soit utile dans le calcul, soit inutile, mais jamais à moitié utile. On veut éradiquer du réseau les chemins inutiles. Si je veux calculer avec un réseau de neurones le nombre de fruits, et que j'ai en entrée le nombre de pommes, d'oranges et de carottes, le neurone carotte ne sert à rien dans le calcul. Sauf que c'est pas à moi de décider ce qui est utile ou pas. C'est au réseau de trouver lui-même quelles sont les données utiles. Donc le réseau idéal devra donner un poids fort (0,999) à pomme et à orange, et il devra donner un poids faible au neurone carottes (0,0001). Mais surtout ne pas avoir des poids du type 0,5, parce que ça veut dire qu'il n'a pas réussi à déterminer si carotte était utile ou pas pour connaître le nombre de fruits. Bref, à chaque couche, on veut savoir si notre calcul intermédiaire a oui ou non une utilité pour le calcul final.
weight(old) + learning rate * output error * output(neurons i) * output(neurons i+1) * ( 1 - output(neurons i+1) )
weight(old) + on veut modifier le poids actuel, pas le remplacer complètement, donc on part de l'ancien poids, et on l'augmente un peu ou bien on le réduit un peu. On veut converger progressivement vers le réseau optimal. Si on remplace absolument tout à chaque étape, on ne saura pas dire si on va dans la bonne direction / si on s'améliore, parce que le réseau perdrait la "mémoire" de ses précédentes tentatives avec lesquelles comparer la tentative actuelle.
learning rate * c'est un paramètre arbitraire qui dit à quelle vitesse le réseau va prendre en compte ses erreurs, ici le mec a mis 0,25. Si tu mets plus, le réseau va beaucoup prendre en compte ses erreurs pour se corriger ; si tu mets moins le réseau va attendre de commettre beaucoup d'erreurs avant de se dire qu'il faut changer quelque chose. On voit bien dans la formule que plus le learning rate est grand, plus le poids va être modifié.
Il me semble que si le learning rate est grand, le réseau va converger vite, mais pas forcément vers LE réseau optimal. Alors que si le learning rate est faible, le réseau va converger lentement, mais potentiellement il sera à la fin beaucoup plus proche DU réseau optimal.
C'est un juste milieu, il faut expérimenter avec différents learning rates et trouver celui qui a l'air de fournir des résultats acceptables sans avoir à attendre 10 000 ans.
output error * c'est normal qu'il faille modifier le poids d'autant plus que l'erreur est grande. Si le poids est pas bon du tout, il faut le changer beaucoup ; si le poids est juste un petit peu faux, il faut l'ajuster légèrement. C'est le morceau le plus évident de la formule.
output(neurons i) * c'est le résultat de la couche précédente, que le neurone courant multiplie par son poids, le poids qu'on est justement en train d'essayer d'ajuster. Donc si ce résultat (venant de l'amont) était grand, il a une grande incidence sur le résultat de notre neurone courant. Ici il faut bien imaginer que notre neurone courant reçoit plusieurs résultats de la couche en amont : des petits résultats 0.0123 et des grands résultats 0.9987, et que pour chacun de ces résultats qu'on lui fournit, notre neurone courant a un poids. Les résultats de la couche amont (qui sont les entrées de notre neurone courant) n'ont pas tous le même impact sur le résultat produit : les grands résultats auront plus d'impact. Notre neurone courant reçoit 0,00012 0,0001 0,895 0,784, il va multiplier tout ça par des poids et les additionner, eh bien les deux derniers auront beaucoup d'importance dans son calcul, on peut carrément négliger les deux premiers tellement ils sont ridicules. Donc si notre neurone s'est trompé, c'est surtout à cause des branches qui ont fourni les grands résultats, et des poids de ces branches. Les branches qui ont passé les grands résultats sont plus "coupables" de l'erreur que les branches qui ont passé de petits résultats. C'est pourquoi la formule change davantage le poids d'une branche qui a fourni une grande valeur.
output(neurons i+1) * ( 1 - output(neurons i+1) ) cette dernière partie, je la traiterais un en seul bloc. En gros c'est la fonction x*(1-x) appliquée au résultat produit par notre neurone courant. Que fait cette fonction x*(1-x) ? Si on met une valeur extrême dedans, elle sort un petit nombre : 0,01 * 0,99 = 0,0099 ; et si on lui donne une valeur moyenne, elle sort un grand nombre : 0,5 * 0,5 = 0,25. Il faut bien voir que 0,25 est beaucoup plus grand que 0,0099. Donc en gros, le poids sera d'autant plus modifié que notre neurone courant a produit un résultat moyen. Ici, mon interprétation est qu'on veut que notre neurone produise des résultats bien tranchés (0,001 ou 0,999) et pas des 0,5 tout mous. Comme s'il y avait un postulat qu'un neurone était soit utile dans le calcul, soit inutile, mais jamais à moitié utile. On veut éradiquer du réseau les chemins inutiles. Si je veux calculer avec un réseau de neurones le nombre de fruits, et que j'ai en entrée le nombre de pommes, d'oranges et de carottes, le neurone carotte ne sert à rien dans le calcul. Sauf que c'est pas à moi de décider ce qui est utile ou pas. C'est au réseau de trouver lui-même quelles sont les données utiles. Donc le réseau idéal devra donner un poids fort (0,999) à pomme et à orange, et il devra donner un poids faible au neurone carottes (0,0001). Mais surtout ne pas avoir des poids du type 0,5, parce que ça veut dire qu'il n'a pas réussi à déterminer si carotte était utile ou pas pour connaître le nombre de fruits. Bref, à chaque couche, on veut savoir si notre calcul intermédiaire a oui ou non une utilité pour le calcul final.
Re: Les mensonges de la presse
Purée merci beaucoup. 
Re: Les mensonges de la presse
Allez je la mets là aussi :
- Roi of the Suisse
- Messages : 2105
- Enregistré le : 28 avr. 2019, 23:38
- Contact :
Re: Les mensonges de la presse
Ah ça me fait chaud au coeur que ça t'indigne aussi, trottaire, parce que je craignais que la malhonnêteté ne t'indignait que lorsqu'elle était à gauche de l'échiquier politique, car tu sembles parfois exercer un débunk asymétrique, mais en fait non, tu as le coeur pur, tu es un authentique amoureux de la vertu. Allez Louya. Béni sois-tu.
